1. 概览
在本实验中,您将学习如何将卷积层组装到能够识别花朵的神经网络模型中。这一次,您将自己从头开始构建模型,并利用 TPU 的强大功能在几秒钟内完成模型训练,并迭代其设计。
本实验包含关于卷积神经网络的必要理论解释,非常适合开发者学习深度学习知识。
本实验是“TPU 上的 Keras”的第 3 部分系列视频您可以按以下顺序执行这些操作,也可以单独执行这些操作。
- TPU 速度数据流水线:tf.data.Dataset 和 TFRecords
- 您的第一个具有迁移学习功能的 Keras 模型
- [本实验] 包含 Keras 和 TPU 的卷积神经网络
- 现代卷积神经网络、squeezenet、Xception,以及 Keras 和 TPU

学习内容
- 使用 Keras Sequential 模型构建卷积图像分类器。
- 在 TPU 上训练 Keras 模型
- 使用合适的卷积层对模型进行微调。
反馈
如果您发现此 Codelab 中存在错误,请告诉我们。您可以通过 GitHub 问题 [反馈链接] 提供反馈。
2. Google Colaboratory 快速入门
此实验使用 Google 协作工具,无需您进行任何设置。Colaboratory 是一个用于教学的在线笔记本平台。它提供免费的 CPU、GPU 和 TPU 训练。

您可以打开此示例笔记本并运行几个单元,以熟悉 Colaboratory。
选择 TPU 后端
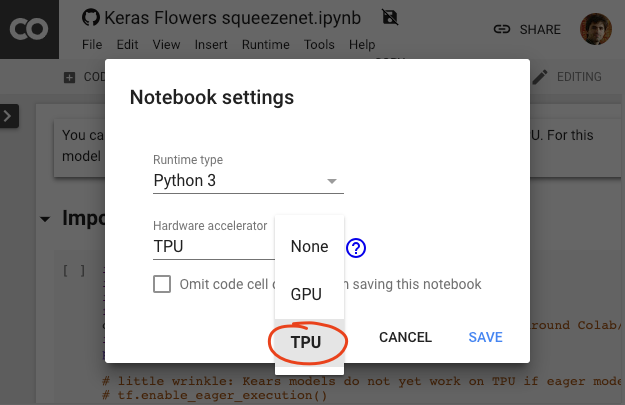
在 Colab 菜单中,选择运行时 >更改运行时类型,然后选择 TPU。在此 Codelab 中,您将使用一个支持硬件加速训练的强大 TPU(张量处理单元)。首次执行时会自动连接到运行时,您也可以使用“Connect”按钮。
笔记本执行

通过点击单元格并使用 Shift-ENTER 一次执行一个单元格。您还可以使用 Runtime >运行全部
目录

所有笔记本都有一个目录。您可以使用左侧的黑色箭头将其打开。
隐藏单元格

部分单元格将仅显示标题。这是 Colab 特有的笔记本功能。您可以双击它们来查看其中的代码,但通常不是很有趣。通常是支持函数或可视化函数。您仍然需要运行这些单元才能定义其中的函数。
Authentication

如果您使用已获授权的账号进行身份验证,则 Colab 可以访问您不公开的 Google Cloud Storage 存储分区。上面的代码段将触发身份验证过程。
3. [INFO] 什么是张量处理单元 (TPU)?
简述

使用 Keras 在 TPU 上训练模型的代码(如果 TPU 不可用,则回退到 GPU 或 CPU):
try: # detect TPUs
tpu = tf.distribute.cluster_resolver.TPUClusterResolver.connect()
strategy = tf.distribute.TPUStrategy(tpu)
except ValueError: # detect GPUs
strategy = tf.distribute.MirroredStrategy() # for CPU/GPU or multi-GPU machines
# use TPUStrategy scope to define model
with strategy.scope():
model = tf.keras.Sequential( ... )
model.compile( ... )
# train model normally on a tf.data.Dataset
model.fit(training_dataset, epochs=EPOCHS, steps_per_epoch=...)
我们今天将使用 TPU 以交互速度(每次训练运行的分钟数)构建和优化花卉分类器。

为什么选择 TPU?
现代 GPU 是围绕可编程“核心”组织的,这是一种非常灵活的架构,可处理各种任务,如 3D 渲染、深度学习、物理模拟等。另一方面,TPU 可将经典矢量处理器与专用矩阵乘法单元配对,并擅长处理大型矩阵乘法占主导的任何任务,例如神经网络。

插图:以矩阵乘法表示的密集神经网络层,通过神经网络同时处理一批 8 张图片。请执行一行 x 列乘法运算,以验证这是否确实对图片的所有像素值进行加权和。卷积层也可以表示为矩阵乘法,尽管它有点复杂( 此处的说明,第 1 部分)。
硬件
MXU 和 VPU
TPU v2 核心由一个矩阵乘法单元 (MXU) 组成,该单元针对所有其他任务(例如激活、softmax 等)运行矩阵乘法和矢量处理单元 (VPU)。VPU 负责处理 float32 和 int32 计算。另一方面,MXU 以混合精度 16-32 位浮点格式运行。

混合精度浮点数和 bfloat16
MXU 使用 bfloat16 输入和 float32 输出计算矩阵乘法。中间累积以 float32 精度执行。

神经网络训练通常能够抵抗因浮点精度降低而引入的噪声。在某些情况下,噪声甚至有助于优化器收敛。16 位浮点精度一直以来都用于加快计算速度,但 float16 和 float32 格式却截然不同。将精度从 float32 降低至 float16,通常会导致上溢和下溢。虽然存在解决方案,但通常需要执行额外的操作才能使 float16 正常运行。
因此,Google 在 TPU 中引入了 bfloat16 格式。bfloat16 是截断的 float32,其指数位和范围与 float32 完全相同。再加上 TPU 会计算与 bfloat16 输入(但 float32 输出)混合精度的矩阵乘法,这意味着通常无需更改代码即可从降低精度的性能提升中受益。
脉冲阵列
MXU 使用所谓的“脉动阵列”在硬件中实现矩阵乘法数据元素流经硬件计算单元数组的架构。(在医学中,“收缩性”是指心脏收缩和血流,这里指的是数据的流动。)
矩阵乘法的基本元素是两个矩阵中的一条直线与另一个矩阵的列之间的点积(请参阅本节顶部的图示)。对于矩阵乘法 Y=X*W,结果中的一个元素将是:
Y[2,0] = X[2,0]*W[0,0] + X[2,1]*W[1,0] + X[2,2]*W[2,0] + ... + X[2,n]*W[n,0]
在 GPU 上,可以将这个点积编程为 GPU“核心”然后在尽可能多的“核心”上执行来尝试同时计算所生成矩阵的每个值。如果生成的矩阵为 128x128 大,则需要 128x128=16000 个“核心”这通常是不可行的最大的 GPU 大约有 4000 个核心。另一方面,TPU 使用 MXU 中的计算单元的最低要求硬件:仅使用 bfloat16 x bfloat16 => float32 个乘积累加器,没有任何其他用途。这些矩阵非常小,因此 TPU 可以在 128x128 MXU 中实现 16K 并一次性处理此矩阵乘法。
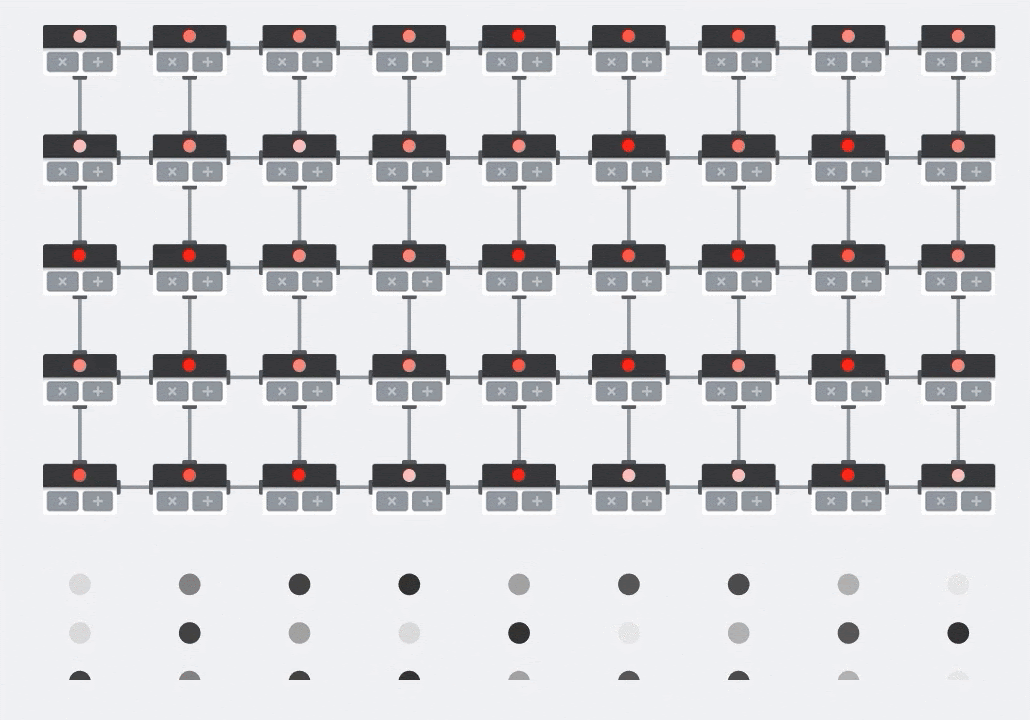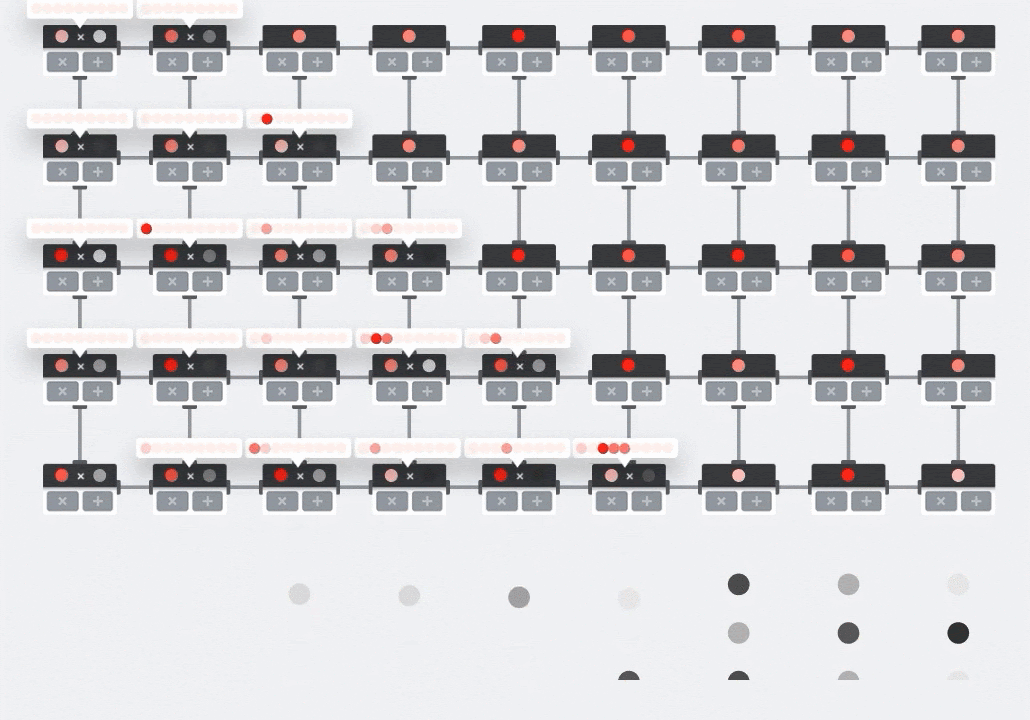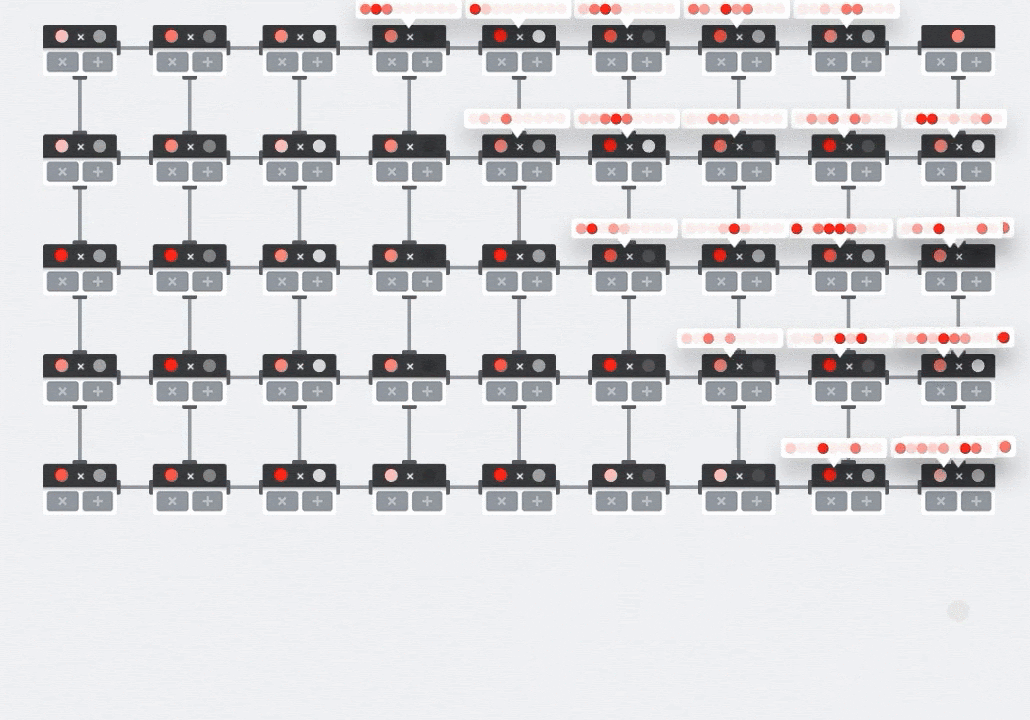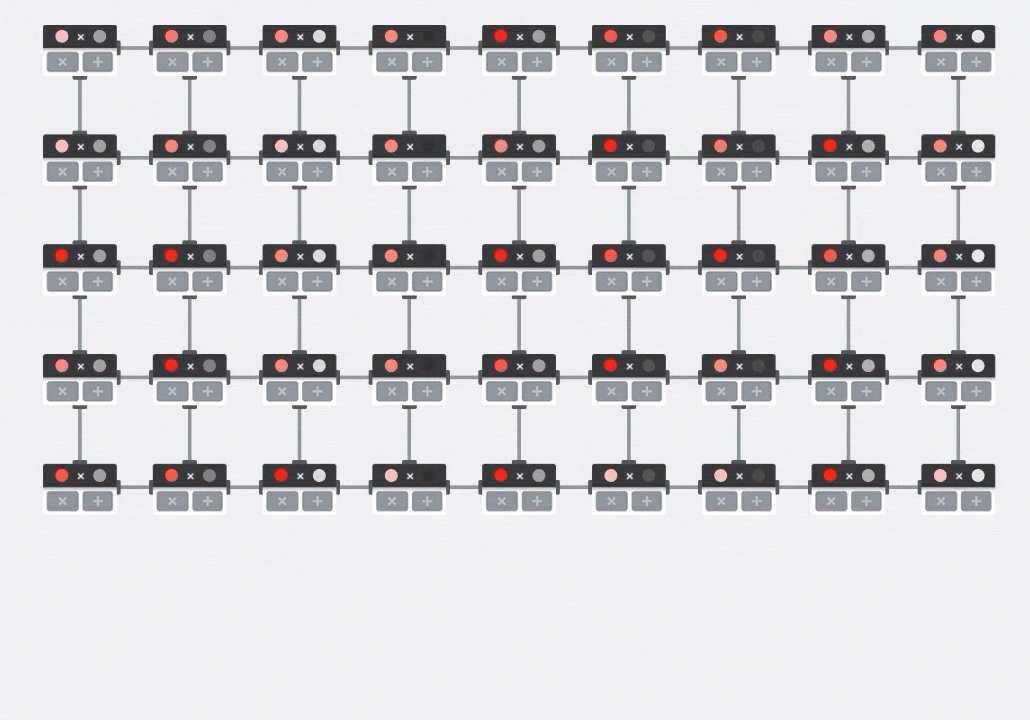
插图:MXU 收缩阵列。计算元素是乘加累加器。一个矩阵的值被加载到数组中(红点)。另一个矩阵的值流过该数组(灰点)。垂直线会将值向上传播。水平线会传播部分总和。留给用户做练习,以便验证当数据流过数组时,您会得到右侧矩阵乘法的结果。
除此之外,虽然点积是根据 MXU 计算的,但中间求和只是在相邻的计算单元之间流动。它们不需要在内存甚至寄存器文件中存储和检索。最终结果是,在计算矩阵乘法时,TPU 脉动阵列架构具有明显的密度和功率优势,并且在计算矩阵乘法时,也比 GPU 具有明显的速度优势。
Cloud TPU
当您请求一个“Cloud TPU v2"在 Google Cloud Platform 上,您会得到一个配有 PCI 连接 TPU 板的虚拟机 (VM)。TPU 板有四个双核 TPU 芯片。每个 TPU 核心都有一个 VPU(矢量处理单元)和 128x128 MXU(矩阵乘法单元)。这个“Cloud TPU”通常通过网络连接到请求它的虚拟机。因此,整个过程如下所示:

图解:具有网络连接的“Cloud TPU”的虚拟机加速器"Cloud TPU"它由一个虚拟机组成,虚拟机配有 PCI 连接的 TPU 板,板上装有四个双核 TPU 芯片。
TPU Pod
在 Google 的数据中心中,TPU 连接到高性能计算 (HPC) 互连,这使得它们看起来就像一个超大加速器。Google 将其称为 Pod,它们最多可包含 512 个 TPU v2 核心或 2048 个 TPU v3 核心。

图解:TPU v3 Pod。通过 HPC 互连连接的 TPU 板和机架。
在训练期间,梯度通过全归约算法在 TPU 核心之间交换(此处充分说明了全归约)。正在训练的模型可以通过使用大批量大小进行训练来充分利用硬件。

图解:在 Google TPU 的二维环形网状网 HPC 网络上使用全约化算法在训练期间同步梯度。
软件
大批量训练
理想的 TPU 批次大小是每个 TPU 核心 128 个数据项,但硬件已经可以显示出每个 TPU 核心 8 个数据项的良好利用率。请注意,一个 Cloud TPU 有 8 个核心。
在此 Codelab 中,我们将使用 Keras API。在 Keras 中,您指定的批次是整个 TPU 的全局批次大小。您的批次将自动拆分为 8 个,并在 TPU 的 8 个核心上运行。

如需了解其他性能提示,请参阅 TPU 性能指南。对于非常大的批次大小,某些模型可能需要特别注意,请参阅 LARSOptimizer 了解详情。
幕后探秘:XLA
TensorFlow 程序定义计算图。TPU 不会直接运行 Python 代码,而是运行由 Tensorflow 程序定义的计算图。在后台,一个名为 XLA(加速线性代数编译器)的编译器将计算节点的 Tensorflow 图转换为 TPU 机器代码。此编译器还可以对您的代码和内存布局执行许多高级优化。编译会在工作发送到 TPU 时自动进行。您无需在 build 链中明确包含 XLA。

图解:为了在 TPU 上运行,您的 Tensorflow 程序定义的计算图会先转换为 XLA(加速线性代数编译器)表示法,然后再由 XLA 编译成 TPU 机器代码。
在 Keras 中使用 TPU
从 Tensorflow 2.1 开始,可通过 Keras API 支持 TPU。Keras 支持适用于 TPU 和 TPU Pod。下面是一个适用于 TPU、GPU 和 CPU 的示例:
try: # detect TPUs
tpu = tf.distribute.cluster_resolver.TPUClusterResolver.connect()
strategy = tf.distribute.TPUStrategy(tpu)
except ValueError: # detect GPUs
strategy = tf.distribute.MirroredStrategy() # for CPU/GPU or multi-GPU machines
# use TPUStrategy scope to define model
with strategy.scope():
model = tf.keras.Sequential( ... )
model.compile( ... )
# train model normally on a tf.data.Dataset
model.fit(training_dataset, epochs=EPOCHS, steps_per_epoch=...)
在此代码段中:
TPUClusterResolver().connect()用于查找网络上的 TPU。它无需参数即可在大多数 Google Cloud 系统(AI Platform 作业、Colaboratory、Kubeflow、通过“ctpu up”实用程序创建的深度学习虚拟机)上运行。由于 TPU_NAME 环境变量,这些系统知道其 TPU 的位置。如果您手动创建 TPU,请设置 TPU_NAME env。变量或者使用显式参数TPUClusterResolver(tp_uname, zone, project)调用TPUClusterResolverTPUStrategy是实现分布和“all-reduce”的部分梯度同步算法。- 系统会通过范围应用策略。必须在策略 scope() 中定义模型。
tpu_model.fit函数需要 tf.data.Dataset 对象作为 TPU 训练的输入。
常见的 TPU 移植任务
- 虽然在 Tensorflow 模型中加载数据的方法有很多,但对于 TPU,必须使用
tf.data.DatasetAPI。 - TPU 速度非常快,在 TPU 上运行时,数据提取常常成为瓶颈。TPU 性能指南中提供了一些工具,可用于检测数据瓶颈和其他性能提示。
- int8 或 int16 数字被视为 int32。TPU 没有在少于 32 位上运行的整数硬件。
- 不支持某些 TensorFlow 操作。点击此处查看列表。好消息是,此限制仅适用于训练代码,即前向和后向传递模型。您仍然可以在数据输入流水线中使用所有 TensorFlow 操作,因为它们将在 CPU 上执行。
- TPU 不支持
tf.py_func。
4. [INFO] 神经网络分类器 101
简述
如果你已经知道下一段落中以粗体显示的所有术语,可以接着进行下一个练习。如果您刚开始接触深度学习,欢迎继续阅读。
对于构建为一系列层的模型,Keras 可提供 Sequential API。例如,使用 3 个密集层的图片分类器可以在 Keras 中编写为:
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[192, 192, 3]),
tf.keras.layers.Dense(500, activation="relu"),
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(5, activation='softmax') # classifying into 5 classes
])
# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy']) # % of correct answers
# train the model
model.fit(dataset, ... )

密集神经网络
这是最简单的图像分类神经网络。它由“神经元”组成并层层叠放在一起。第一层处理输入数据,并将其输出馈送到其他层。称为“密集”因为每个神经元都与前一层中的所有神经元相连。

您可以将图片馈送到此类网络中,方法是将其所有像素的 RGB 值展平为长矢量并将其用作输入。这不是图片识别的最佳技术,但我们稍后会对其进行改进。
神经元、激活、RELU
一个“神经元”计算所有输入的加权和,然后添加一个名为“偏差”的值并通过所谓的“激活函数”提供结果。权重和偏差最初是未知的。它们会随机初始化并“学习”通过使用大量已知数据训练神经网络来实现。

最常用的激活函数称为修正线性单元的 RELU。如上图所示,这是一个非常简单的函数。
Softmax 激活
上述网络以 5 神经元层结尾,因为我们将花卉分为 5 类(玫瑰、郁金香、蒲公英、雏菊、向日葵)。中间层的神经元使用经典的 RELU 激活函数进行激活。不过,在最后一层中,我们需要计算 0 到 1 之间的数字,表示这朵花是玫瑰、郁金香等的概率。为此,我们将使用一个名为“softmax”的激活函数。
对向量应用 Softmax 的方法是取每个元素的指数,然后对向量进行归一化,通常使用 L1 范数(绝对值总和),使值加起来为 1,并且可以解释为概率。


交叉熵损失
现在,我们的神经网络可以根据输入图片生成预测,接下来我们需要衡量预测的好坏,即网络告诉我们的信息与正确答案之间的距离,通常称为“标签”。请记住,数据集中的所有图片都有正确的标签。
任何距离都有效,但对于分类问题而言,所谓的“交叉熵距离”是最有效的。我们将这种情况称为错误或“损失”。函数:

梯度下降法
“训练”神经网络实际上意味着使用训练图片和标签来调整权重和偏差,以便最大限度地降低交叉熵损失函数的值。其运作方式如下。
交叉熵是训练图片的权重、偏差、像素及其已知类别的函数。
如果我们计算交叉熵相对于所有权重和所有偏置的偏导数,就会得到一个“梯度”,该梯度针对给定图像、标签以及权重和偏差的现值进行了计算。请记住,我们可以有数百万个权重和偏差,因此计算梯度声就像是大量的工作。幸运的是,Tensorflow 可以为我们做到这一点。渐变的数学属性是它指向“向上”。由于我们想去交叉熵较低的地方,因此会前往相反的方向。我们以梯度的分数更新权重和偏差。然后,我们在训练循环中使用下一批训练图片和标签重复执行相同的操作。我们希望这可以收敛到交叉熵极低的位置,但无法保证此最小值是唯一的。

小批量和动量
您可以仅对一张样本图片计算梯度,并立即更新权重和偏差,但对一批 128 张图片(例如 128 张图片)执行此操作将产生一个梯度,该梯度可以更好地表示不同样本图片施加的限制,因此可能会更快地收敛于解决方案。小批次的大小是一个可调整的参数。
这种技术有时称为“随机梯度下降”还有一个更实际的好处:使用批量处理还意味着使用较大的矩阵,这些矩阵通常更易于在 GPU 和 TPU 上进行优化。
不过,收敛可能仍然有点混乱,即使梯度矢量都为零,收敛也可能会停止。这是否意味着我们找到了一个最低值?不一定。梯度分量可以为零的最小值或最大值。对于包含数百万个元素的梯度矢量,如果这些元素全部为零,则每个零对应于一个最小值而没有一个对应于最大点的概率非常小。在具有很多维度的空间中,马鞍点很常见,我们不想就此止步。

插图:马鞍点。梯度为 0,但并非在所有方向上的最小值。(图片出处 维基媒体:Nicoguaro - 自创内容,CC BY 3.0)
解决方法是为优化算法增加一些动力,使其不停地驶过马鞍点。
术语库
batch 或 mini-batch:始终对批量训练数据和标签执行训练。这样做有助于算法收敛。“批次”维度通常是数据张量的第一个维度。例如,形状为 [100, 192, 192, 3] 的张量包含 100 张 192x192 像素的图片,每个像素有三个值 (RGB)。
交叉熵损失:分类器中常用的一种特殊损失函数。
密集层:一个神经元层,其中每个神经元都与前一层中的所有神经元连接。
特征:神经网络的输入有时称为“特征”。弄清楚将数据集的哪些部分(或部分组合)馈送到神经网络以获得良好预测结果的过程称为“特征工程”。
labels:“类”的另一种名称在监督式分类问题中,
学习速率:权重和偏差在训练循环的每次迭代中更新时的梯度百分比。
logits:在应用激活函数之前,一层神经元的输出称为“logits”。这个术语来自“逻辑函数”也称为“S 型函数”这曾是最常用的激活函数。"逻辑函数之前的中子输出"已简化为“logits”。
loss:将神经网络输出与正确答案进行比较的误差函数
神经元:计算其输入的加权和,添加偏差并通过激活函数馈送结果。
独热编码:第 3 类(共 5 类)编码为 5 个元素(第三个元素为 1 除外)的向量。
relu:修正的线性单元。一种热门的神经元激活函数。
S 型函数:另一种过去很流行的激活函数,在特殊情况下仍然有用。
softmax:一个作用于向量的特殊激活函数,用于增大最大分量与所有其他分量之间的差值,同时对该向量进行归一化,使其总和为 1,以便将其解释为概率向量。用作分类器中的最后一步。
tensor:“张量”类似于矩阵,但维度数量没有限制。一维张量是一个向量。二维张量就是一个矩阵。然后,您可以得到具有 3 个、4 个、5 个或更多维度的张量。
5. [最新资讯] 卷积神经网络
简述
如果你已经知道下一段落中以粗体显示的所有术语,可以接着进行下一个练习。如果您刚开始接触卷积神经网络,请继续阅读。
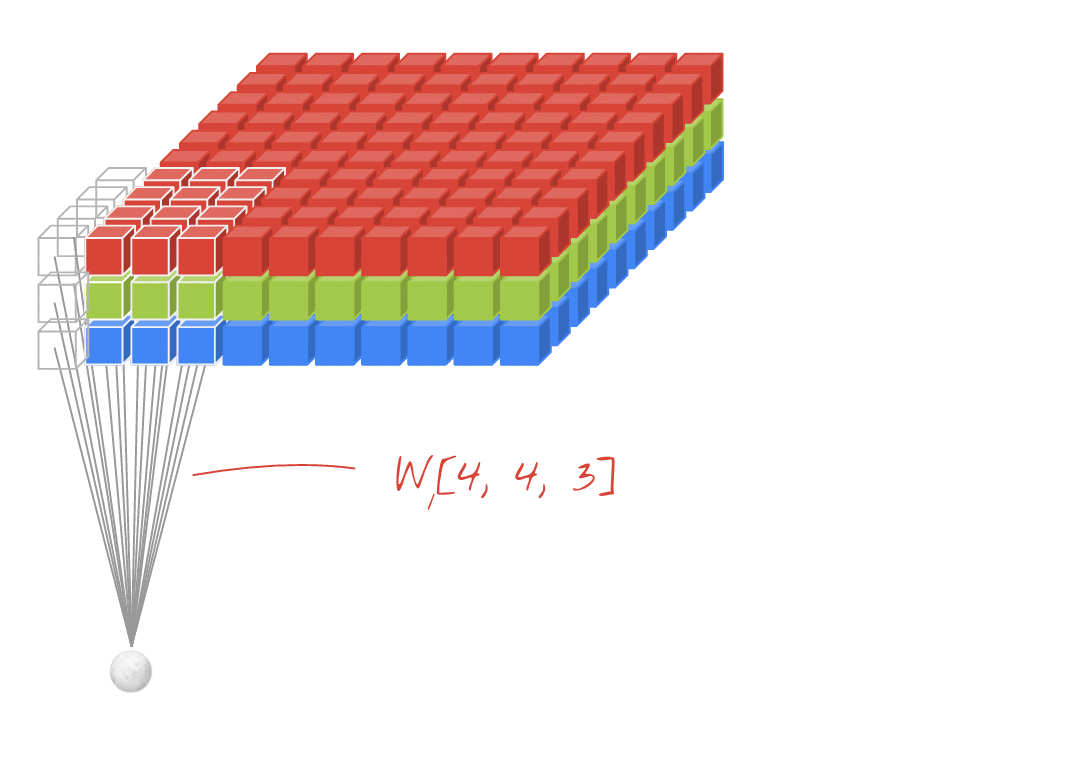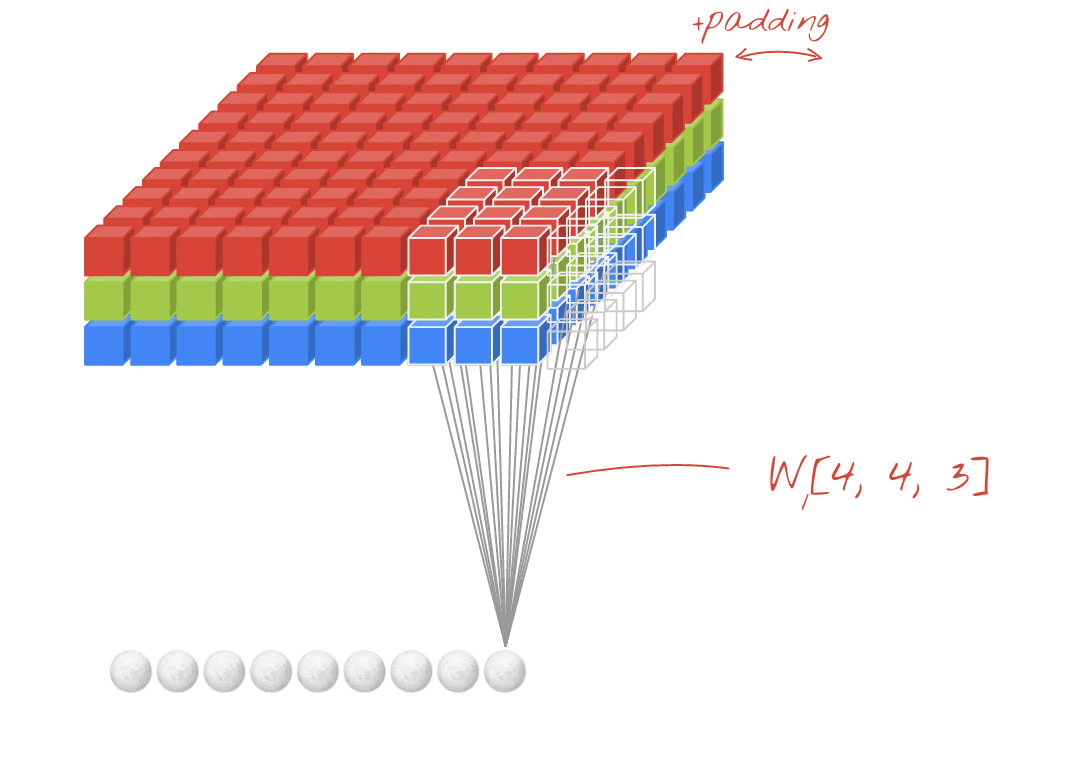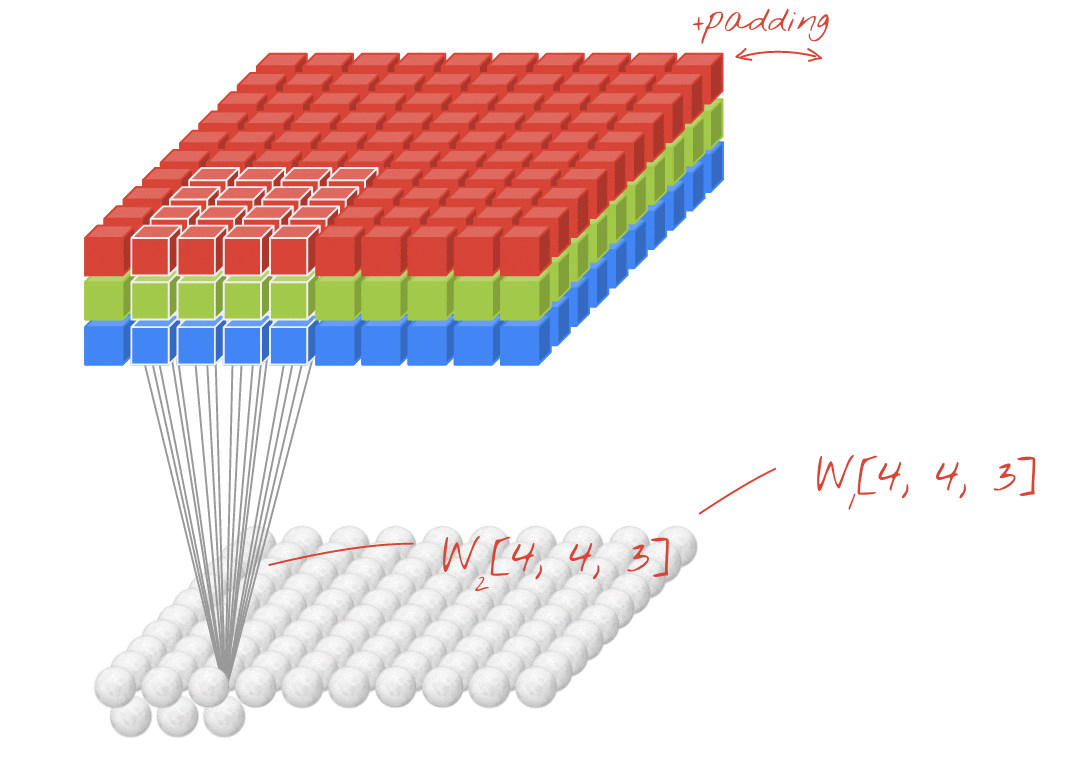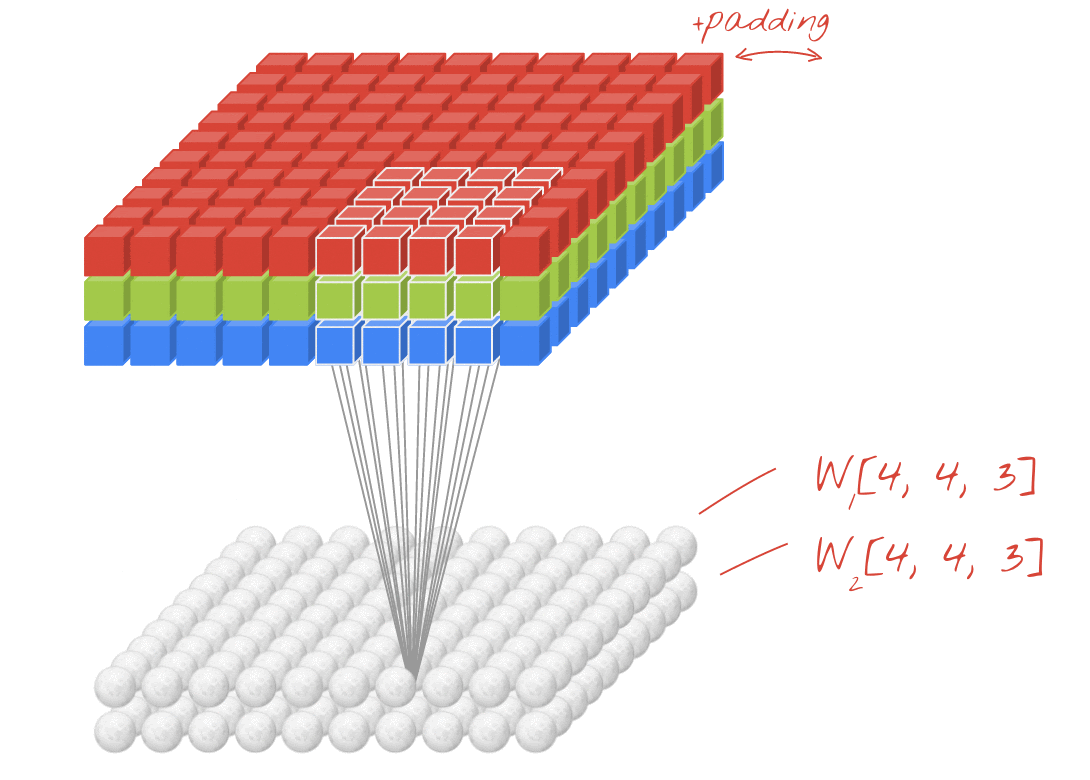
插图:使用两个由 4x4x3=48 个可学习权重组成的连续过滤器来过滤图片。
下面是简单的卷积神经网络在 Keras 中的样子:
model = tf.keras.Sequential([
# input: images of size 192x192x3 pixels (the three stands for RGB channels)
tf.keras.layers.Conv2D(kernel_size=3, filters=24, padding='same', activation='relu', input_shape=[192, 192, 3]),
tf.keras.layers.Conv2D(kernel_size=3, filters=24, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=6, padding='same', activation='relu'),
tf.keras.layers.Flatten(),
# classifying into 5 categories
tf.keras.layers.Dense(5, activation='softmax')
])
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy'])

卷积神经网络基础知识
在卷积网络中的一个层中,一个“神经元”会对紧邻其上的像素进行加权和,只对其上的一小块区域进行加权。它会添加偏差并通过激活函数向和馈送总和,就像常规密集层中的神经元一样。然后,使用相同的权重对整张图片重复此操作。请记住,在密集层中,每个神经元都有自己的权重。在这里,一个“补丁”的权重在图像上两个方向滑动(“卷积”)。输出的值与图像中的像素数一样多(不过边缘部分需要一些内边距)。这是一个使用 4x4x3=48 权重的过滤器的过滤操作。
但是,48 个权重并不够。为了增加自由度,我们使用一组新权重重复同一操作。这样会生成一组新的过滤器输出。我们称之为“频道”通过与输入图像中的 R、G、B 通道类比来比较输出结果。
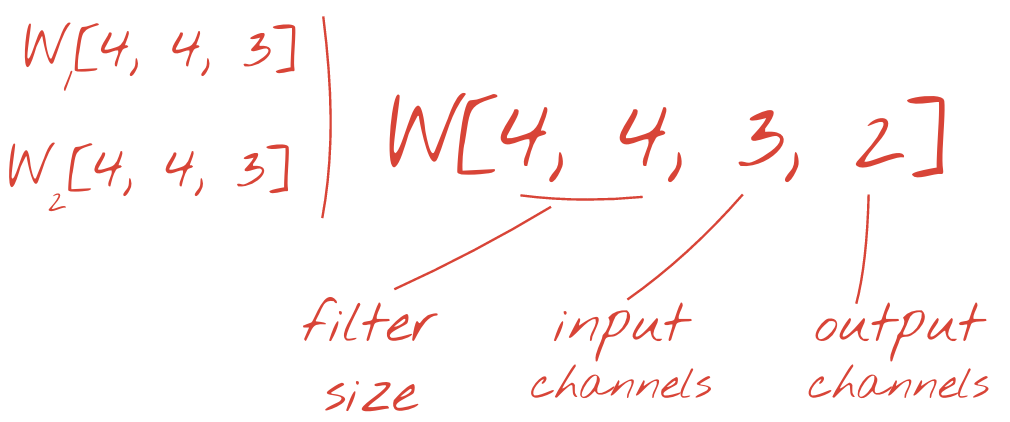
通过添加新维度,将两组(或更多)权重求和为一个张量。这为我们确定了卷积层权重张量的通用形状。由于输入和输出通道的数量是参数,因此我们可以开始堆叠和链接卷积层。
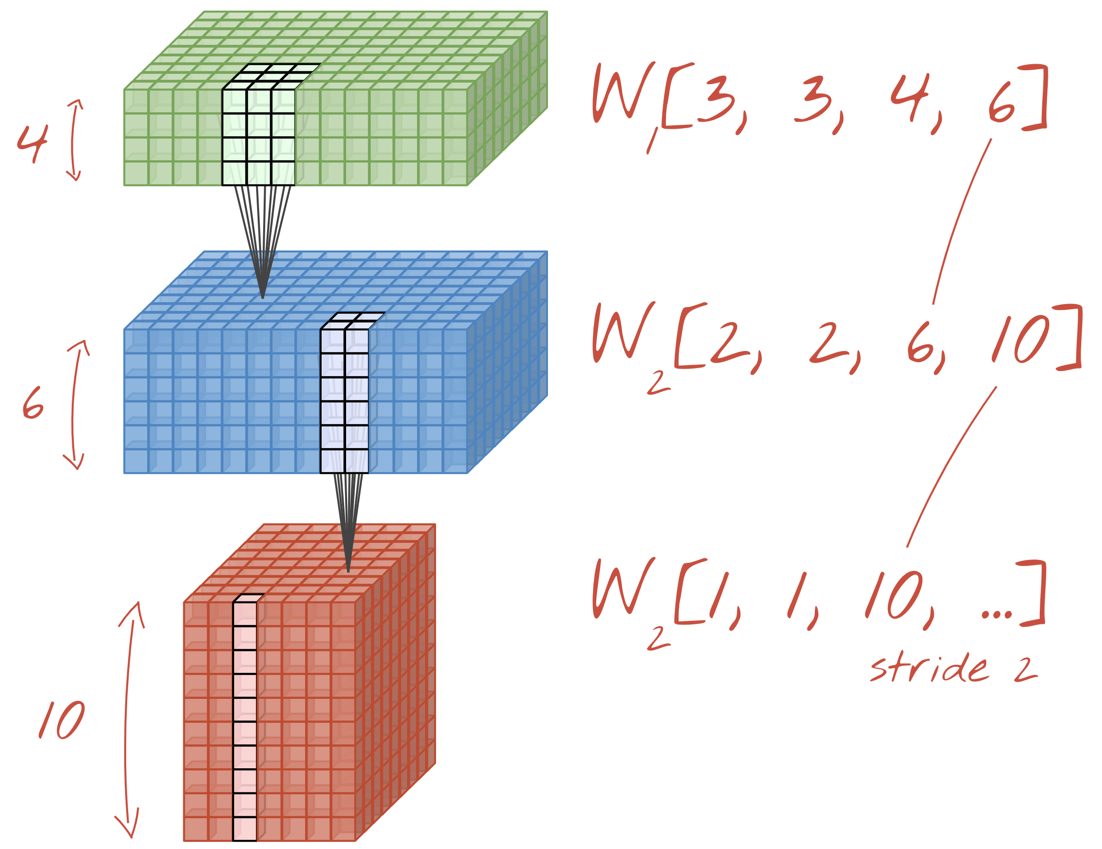
图解:卷积神经网络转换“立方体”将数据转移到其他“立方体”数据。
步进卷积、最大池化
通过以步长 2 或 3 执行卷积,我们还可以在水平维度上缩小生成的数据立方体。您可以采用以下两种常见方式:
- 步进卷积:如上所示的滑动过滤器,但步长 >1
- 最大池化:应用 MAX 操作的滑动窗口(通常采用 2x2 图块,每 2 像素重复一次)

图解:将计算窗口滑动 3 个像素会减少输出值。步长卷积或最大池化(以 2x2 窗口的步长 2 滑动的最大值)是在水平维度上缩小数据立方体的方法。
卷积分类器
最后,我们通过展平最后一个数据立方体并通过密集的 softmax 激活层馈送分类头来附加分类头。典型的卷积分类器可能如下所示:

插图:使用卷积层和 softmax 层的图像分类器。它使用 3x3 和 1x1 过滤条件。maxpool 层会获取最多 2x2 数据点组。分类头通过具有 softmax 激活的密集层来实现。
在 Keras 中
上图中的卷积堆栈可以用 Keras 编写,如下所示:
model = tf.keras.Sequential([
# input: images of size 192x192x3 pixels (the three stands for RGB channels)
tf.keras.layers.Conv2D(kernel_size=3, filters=32, padding='same', activation='relu', input_shape=[192, 192, 3]),
tf.keras.layers.Conv2D(kernel_size=1, filters=32, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=32, padding='same', activation='relu'),
tf.keras.layers.Conv2D(kernel_size=1, filters=32, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=32, padding='same', activation='relu'),
tf.keras.layers.Conv2D(kernel_size=1, filters=32, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=32, padding='same', activation='relu'),
tf.keras.layers.Conv2D(kernel_size=1, filters=32, padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=2),
tf.keras.layers.Conv2D(kernel_size=3, filters=16, padding='same', activation='relu'),
tf.keras.layers.Conv2D(kernel_size=1, filters=8, padding='same', activation='relu'),
tf.keras.layers.Flatten(),
# classifying into 5 categories
tf.keras.layers.Dense(5, activation='softmax')
])
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy'])
6. 您的自定义转化
动手实践
让我们从头开始构建和训练卷积神经网络。使用 TPU 可以使我们实现非常快速的迭代。请打开以下笔记本,执行单元格 (Shift-ENTER),然后按照显示“必须完成的工作”提示操作标签。

Keras_Flowers_TPU (playground).ipynb
目标是超过迁移学习模型 75% 的准确率。该模型具有一个优势,已基于包含数百万张图片的数据集进行预训练,而此处的图片数量只有 3670 张。你能至少配上它吗?
其他信息
有多少层,有多大?
选择层大小更像是一门艺术,而不是一门科学。您必须在参数(权重和偏差)过少和过多之间找到适当的平衡。如果权重太少,神经网络就无法表示花朵形状的复杂性。图像太多,则容易出现“过拟合”,即专业训练图像而无法泛化。如果参数太多,模型的训练速度也会很慢。在 Keras 中,model.summary() 函数可显示模型的结构和参数数量:
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 192, 192, 16) 448
_________________________________________________________________
conv2d_1 (Conv2D) (None, 192, 192, 30) 4350
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 96, 96, 30) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 96, 96, 60) 16260
_________________________________________________________________
...
_________________________________________________________________
global_average_pooling2d (Gl (None, 130) 0
_________________________________________________________________
dense (Dense) (None, 90) 11790
_________________________________________________________________
dense_1 (Dense) (None, 5) 455
=================================================================
Total params: 300,033
Trainable params: 300,033
Non-trainable params: 0
_________________________________________________________________
两点提示:
- 具备多层才是“深度”的因素非常有效。对于这种简单的花卉识别问题,5 到 10 个层比较合理。
- 使用小过滤条件。通常,3x3 过滤器在任何环境下都适用。
- 也可以使用 1x1 过滤器,而且价格便宜。它们并不会真正“过滤”而不是计算渠道的线性组合。不妨用真实的滤镜替代它们。(下一部分将详细介绍“1x1 卷积”。)
- 对于这样的分类问题,频繁使用最大池化层(或步长 > 1 的卷积)进行下采样。您不在乎花朵的位置,只知道它是玫瑰或蒲公英,所以丢失 x 和 y 信息并不重要,过滤较小区域的费用会比较低。
- 过滤器的数量通常与网络末尾的类别数量相似(为什么?请参阅下文中的“全局平均池化”技巧)。如果分类为数百个类别,则应在连续的层中逐步增加过滤器数量。对于包含 5 个类别的花卉数据集,仅用 5 个过滤条件进行过滤是不够的。您可以在大多数图层中使用相同的过滤器数量(例如,32 个过滤器数量),并在最后减少数量。
- 最终的密集层的开销很高。它们的权重可能比所有卷积层加起来的权重更多。例如,即使从 24x24x10 数据点的最后一个数据立方体得到非常合理的输出,一个大小为 100 的神经元密集层也会消耗 24x24x10x100=576,000 个权重 !!!请尽可能考虑周全,或尝试使用全局平均池化方法(请参阅下文)。
全球平均池化
您无需在卷积神经网络的末端使用昂贵的密集层,而是可以将传入数据“立方体”拆分,尽可能多地拆分成多少部分,然后取平均值,然后用 softmax 激活函数输入这些值。这种构建分类头部的方法的权重为 0。在 Keras 中,语法为 tf.keras.layers.GlobalAveragePooling2D().

解决方案
以下是解决方案笔记本。如果您遇到困难,可以使用它。

Keras_Flowers_TPU (solution).ipynb
所学内容
- 🤔? 使用过卷积层
- 🤓? 尝试了最大池化、步长、全局平均池化...
- 😀? 在 TPU 上快速对真实模型进行迭代
请花点时间回想一下这份核对清单。
7. 恭喜!
您已经构建了自己的第一个现代卷积神经网络,对其进行训练后,准确率达到了 80% 以上。得益于 TPU,您只需几分钟即可对其架构进行迭代。请继续完成下一个实验,了解现代卷积架构:
- TPU 速度数据流水线:tf.data.Dataset 和 TFRecords
- 您的第一个具有迁移学习功能的 Keras 模型
- [本实验] 包含 Keras 和 TPU 的卷积神经网络
- 现代卷积神经网络、squeezenet、Xception,以及 Keras 和 TPU
TPU 使用实例
Cloud AI Platform 上提供 TPU 和 GPU:
- 在 Deep Learning VM 上
- 在 AI Platform Notebooks 中
- 在 AI Platform Training 作业中
最后,欢迎您提供反馈。如果您发现此实验中存在错误,或者您认为需要改进,请告诉我们。您可以通过 GitHub 问题 [反馈链接] 提供反馈。

|



